Um bei der heutigen Vielzahl von Optionsscheinen den richtigen zu finden, bedarf es einem soliden Grundverständnis der wichtigsten Kennzahlen. Wenn du diese nicht im Schlaf beherrschst, werden dir entweder die Kurse davonlaufen oder du kaufst einen überteuerten Optionsschein.
Die meisten Finanzzeitschriften enthalten zwar umfangreiche Tabellen mit den wichtigsten Bewertungskriterien, diese sind jedoch meistens aufgrund der hohen Schwankungen (Volatilität) in diesem Marktsegment nicht aktuell und irreführend. Daher ist es wichtig neben soliden Grundkenntnissen auch ein Gefühl für die Preisentwicklung eines Optionsscheines aufzubauen.
Um dir diese Kennzahlen möglichst praxisnah erklären zu können, nutze ich folgendes Beispiel:

Wichtig: Der Kurs eines Optionsscheins setzt sich immer aus zwei Bestandteilen zusammen: Dem Inneren Wert und dem Zeitwert. Das Bezugsverhältnis muss dabei mit berücksichtigt werden. Das Bezugsverhältnis in unserem Beispiel von 0,1 sagt aus, dass 10 Optionsscheine nötig sind, um 1 Aktie zu beziehen.
Inhaltsverzeichnis
Innerer Wert:
Den inneren Wert eines Optionsscheines erhält man, wenn man den Basispreis (engl. Strike) von dem aktuellen Kurs des Basiswertes (Call), bzw. vom Basispreis den aktuellen Kurs des Basiwertes (Put) abzieht. Dabei muss das Bezugsverhältnis (hier 10:1 bzw. 0,1) berücksichtigt werden. Der innere Wert eines Optionsscheins entspricht folglich dem Betrag, den der Inhaber bei sofortiger Ausübung realisieren kann.
- Innerer Wert (Call) = (aktueller Kurs des Basiswertes – Basispreis) x Bezugsverhältnis (für einen Call)
- Innerer Wert (Put) = (Basispreis – aktueller Kurs des Basiswertes) x Bezugsverhältnis (für einen Put)
In meinem Beispiel: Innerer Wert = (27 Euro – 20 Euro) x 0,1 = 0,70 Euro
Zeitwert:
Der Optionsschein notiert aktuell bei 1,10 Euro, davon sind wie wir gerade berechnet haben 0,70 Euro innerer Wert, der Rest von 0,40 Euro ist folglich Zeitwert. Der Optionsschein liegt über seinem inneren Wert, er wird also mit Aufgeld gehandelt.
- Zeitwert = Optionsscheinkurs – Innerer Wert
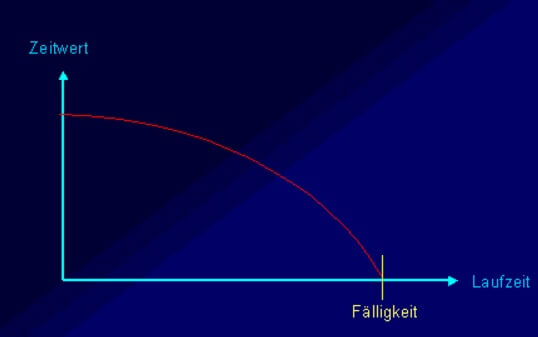
Merke: Selbst wenn der Kurs von Nokia unter den Basispreis von 20 Euro rutschen sollte, so besteht trotzdem die Chance, dass Nokia vor Ende der Laufzeit nochmal diese Marke (Basispreis) überwinden kann. Der Optionswert bzw. Optionsscheinkurs besteht also nur noch aus der Chance bzw. dem Zeitwert. Die Chance nimmt logischerweise mit jedem Tag ab und vermindert damit auch den Optionsscheinkurs.
Welche Zustände gibt es bei Optionsscheinen?
Im Umgang mit Optionsscheinen wird zwischen drei verschiedenen „Zuständen“ des Optionsscheines bezüglich seines Basiswertes unterschieden:
- Im Geld / In the money (ITM): Ein Optionsschein besitzt einen inneren Wert, wenn beim Call (Put) der aktuelle Kurs des Basiswertes über (unter) dem Basispreis liegt. In diesem Fall sagt man, der Optionsschein ist „im Geld“.
- Am Geld / At the money (ATM): Sind Basispreis und aktueller Kurs identisch, hat der Optionsschein keinen inneren Wert. Man sagt, der Optionsschein ist „am Geld“. An diesem Punkt ist der Zeitwert des Optionsscheins am größten.
- Aus dem Geld / Out of the money (OTM): Auch keinen inneren Wert hat ein Optionsschein, wenn der aktuelle Kurs des Basiswertes unter (über) dem Basispreis des Calls (Puts) liegt.
Folgende Grafik zeigt nochmal die Entwicklung des Zeitwerts:
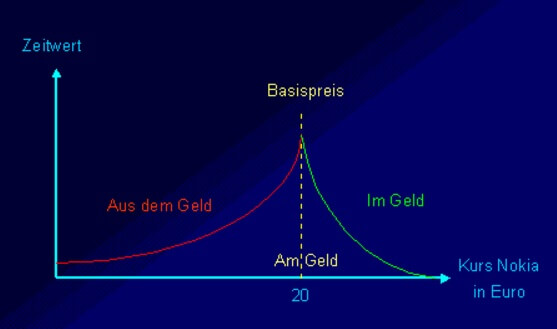
Merke: Ist der Optionsschein am Geld, also der Kurs des Basiswertes gleich dem Basispreis, so ist der Zeitwert am größten. In unserem Beispiel wäre das der Fall, wenn der Kurs von Nokia exakt bei 20 Euro steht, da dies der Basispreis des Calls ist.
Aufgeld:
Das Aufgeld gibt an, um wie viel Prozent die Aktie (Basiswert) steigen muss, bis der Bezug der Aktie durch die Ausübung des Optionsscheines genauso teuer ist wie der direkte Kauf der Aktie an der Börse. Anders ausgedrückt: Um wieviel Prozent der Basiswert bis zur Fälligkeit des Optionsscheins steigen (Call) bzw. fallen (Put) muss, damit der Investor gegenüber seinem Einstiegskurs keinen Verlust erleidet.
Es wird häufig auch als Prämie oder Agio bezeichnet und berechnet sich wie folgt:
- Formel Aufgeld prozentual (Call): ((Optionsscheinkurs * Bezugsverhältnis + Basispreis / Kurs des Basiswerts) – 1) * 100
- Formel Aufgeld prozentual (Put): ((Optionsscheinkurs * Bezugsverhältnis – Basispreis / Kurs des Basiswerts) + 1) * 100
Merke: Damit das Aufgeld bei unterschiedlichen Laufzeiten vergleichbar ist, wird dieses häufig auf eine Laufzeit von einem Jahr hochgerechnet. -> Aufgeld p. a.
Bezogen auf das Beispiel Nokia ergibt sich folglich ein prozentuales Aufgeld von:
- ((((1,10 * 10 / 1) + 20) / 27) – 1) * 100 = 14.81%
Die Aktie Nokia muss also bis zum Laufzeitende um 14,81% auf 31 Euro steigen, damit du keinen Verlust erleidest.
Dieser so genannte Break Even-Point lässt sich folgendermaßen errechnen:
- Break Even-Point (Call): Basispreis + Optionsscheinkurs * Bezugsverhältnis
- Break Even-Point (Put): Basispreis – Optionsscheinkurs * Bezugsverhältnis
Für unser Beispiel bedeutet das: 20 + ((1,10 * 10) / 1) = 31 Euro.
Wie funktioniert der Hebeleffekt?
Die Hebelwirkung ist der eigentliche Reiz jedes Optionsscheininhabers. Sie bewirkt, dass eine Kursveränderung des Basiswertes eine prozentual stärkere Kursveränderung des Optionsscheins auslöst. Man „hebelt“ also im Sinne des Wortes mit einem „kleinen“ Betrag eine „große“ Summe.
Formel für den Hebel:
- Hebel = (aktueller Basiskurs * Bezugsverhältnis)/OS-Kurs
Werfen wir nochmal ein Blick auf das Beispiel:

Der Optionsschein hat also einen Hebel von:
- (27 Euro x 0,1) / 1,10 Euro = 2,45
Wichtig: Der Hebel sagt lediglich aus wieviel „mehr“ Geld man mit einem Optionsschein hebelt im Gegensatz zum direkten Kauf der Aktie. Er berücksichtigt dabei nicht den Zeitwert und sollte daher in der Praxis nicht zur Berechnung der Optionsschein-Performance genutzt werden. Um eine realistische Entwicklung des Optionsscheins gegenüber der Aktie zu berechnen, brauchst du das Delta.
Dynamischen Kennzahlen von Optionsscheinen
Nachdem ich dir die Grundlegenden Kennzahlen von Optionsscheinen vorgestellt habe, zeige ich dir hier die dynamischen Kennzahlen von Optionsscheinen. Los gehts:
Was ist das Delta?
Das Delta ist eine der wichtigsten Kennzahlen und wird mit der komplexen Black-Scholes-Formel oder einem anderen Optionspreismodell berechnet. In der Praxis empfehle ich dir daher, diese mit Hilfe eines Optionsscheinrechners zu kalkulieren oder auf der Internetseite des Emittenten nachzuschlagen.
Das Delta gibt die effektive Veränderung oder auch Sensitivität des Optionsscheins zum Kurs des Basiswerts an. Bei einem Kaufoptionsschein (Call) bewegt sich das Delta zwischen 0 und 1. Das Delta einer Verkaufsoption (Put) hingegen pendelt zwischen 0 und -1.
Beispiel: Wenn dein Nokia-Call genau „am Geld“ steht, dann entspricht der Basispreis dem Kurs des Basiswerts. Nokia notiert also bei 20 Euro. Dein Optionsschein hat nun ein Delta von 0,5. Wenn Nokia jetzt um eine Geldeinheit steigt, also 1 Euro höher bei 21 Euro notiert, so steigt dein Optionsschein um 0,5 dieser Geldeinheit. Unter Berücksichtigung des Bezugsverhältnises also um 0,05 Euro.
Merke: Das Optionsschein-Delta ist um so niedriger, je weiter der Optionsschein „aus dem Geld“ ist, und um so höher, je weiter der Optionsschein „ins Geld“ kommt. Exakt „am Geld“ beträgt das Delta 0,5.
Eines sehr kleines Delta bedeutet folglich, das der Optionsschein weit „aus dem Geld“ ist und kaum auf die Veränderungen des Basiswertes reagiert. Wenn das Delta hingegen fast 1 ist, so bewegen sich Basiswert und Optionsschein fast synchron, da der Optionsschein weit „im Geld“ ist.
Das Delta bringt somit auch die Ausübungswahrscheinlichkeit zum Ausdruck. Ein Optionsschein mit Delta von 0,8 hat eine Ausübungswahrscheinlichkeit von 80%, damit liegt die Wahrscheinlichkeit eines Totalverlustes (Nichtausübung) bei 20%.
Die entscheidendste Hilfe liefert das Delta durch Verrechnung mit dem bereits Hebel => dem Omega
Was ist das Omega?
Das Omega, auch theoretischer oder effektiver Hebel genannt, präzisiert den Hebel und gibt die tatsächliche Hebelleistung eines Optionsscheins wieder.
Formel: Omega = Delta * Hebel
Merke: In der Praxis kann mit dem Omega die effektive Veränderung des Optionsscheins gegenüber dem Basiswert aufgestellt werden. Wenn also der Basiswert um 2 % steigt und ein Omega von 5 vorliegt, so wird der Optionsschein um 5 x 2% = 10 % steigen.
Wichtig: Einer der häufigsten Anfängerfehler ist das Gleichsetzen des Hebels mit dem Omega. Dies kann bei Optionsscheinen, die extrem weit „aus dem Geld“ liegen, zu hohen Verlusten führen. Merk dir als Faustregel, dass Optionsscheine mit einem Delta kleiner 0,2 meistens so weit aus dem Geld liegen, dass sie auf die Bewegungen des Basiswerts nur gering reagieren und somit nur noch ihren Zeitwert abbauen.
In der täglichen Praxis spielt das Omega im Gegensatz zum Hebel eine entscheidende Rolle. Der Hebel hat kaum Aussagekraft bezüglich der zukünftigen Kursentwicklung des Optionsscheins und kann daher in der täglichen Praxis vernachlässigt werden.
Was ist das Theta?
Wie du bereits weißt besteht der Kurswert eines Optionscheins aus dem inneren Wert und dem Zeitwert. Je weiter sich der Optionsscheinkurs dem Laufzeitende nähert, umso weniger besteht dieser aus Zeitwert. Diesen Zeitwertverfall bezeichnet man als Theta. Er wird meistens auf wöchentlicher Basis ermittelt und gibt dementsprechend an, wieviel Prozent bzw. Geldeinheiten der Optionsschein pro Woche infolge des Zeitwertverlustes an Wert verliert.
Beispiel: Ein Wochentheta von beispielsweise -0,07 bedeutet, dass der Optionsschein bei gleichbleibenden Marktverhältnissen 0,07 Euro pro Woche an Wert abgibt.
Wichtig: Bei nur noch sehr kurz laufenden Optionsscheinen ist der Zeitwertverfall am größten, insbesondere bei am Geld notierenden Optionsscheinen, da diese den höchstens Zeitwert aufweisen.
Die folgende Grafik zeigt den zunehmenden Zeitwertverfall eines Optionsscheines gegen Laufzeitende: