Es gibt unterschiedliche Kennzahlen, durch die sich Anleger ein Bild über die aktuelle Bewertung eines Optionsscheins machen können, wodurch sie das zukünftige Kursverhalten analysieren können. Da diese Kennzahlen aus dem griechischen Alphabet entstammen werden sie auch kurz Griechen genannt.
Das Theta
Der Wertverlust einer Option durch den Ablauf der Zeit wird durch die Kennzahl Theta gemessen. Mathematisch ist Theta die erste Ableitung des Optionspreismodells nach der Restlaufzeit. Theta gibt an, um wie viel der Wert des Optionsscheins sinkt, wenn sich die Restlaufzeit um eine Einheit verringert. Als Einheit wird dabei üblicherweise ein Tag oder eine Woche verwendet. Theta sollte dabei stets mit negativem Vorzeichen angegeben werden, da der Wert einer Option mit abnehmender Restlaufzeit geringer wird. Ein Wochentheta von -0,08 bedeutet also, dass der Wert des Optionsscheins zur Zeit innerhalb einer Woche theoretisch um 0,08 Euro fällt, wenn alle anderen Faktoren unverändert bleiben. Da man bei dieser absoluten Angabe des Theta den Zeitwertverlust aber oft unterschätzt, wird häufig das „prozentuale Wochentheta“ angegeben: Hier bedeutet also beispielsweise ein Wert von -3,75, dass der Optionsschein pro Woche allein durch den Zeitwertverlust 3,75 % an Wert verliert!
Insbesondere bei Scheinen aus dem Geld oder am Geld wächst das Theta zum Ende der Laufzeit hin rasant an. Solche Scheine bestehen vollständig oder großteils aus Zeitwert, und der hat am Laufzeitende nun mal bei 0 zu stehen. Wenn man keine absoluten Kurzfristspekulationen vor hat, sollte man Scheine mit einer Restlaufzeit von zwei Monaten und weniger meiden. Aber auch bei langfristigen Engagements kann der Zeitwert an den Gewinnen knabbern oder die Verluste erhöhen. Faustregel: Leg fest, bis wann du das Kursziel deines Basiswertes erwartest, und wähle dann als Laufzeit etwa das 1,5fache, bei kürzeren Laufzeiten das Doppelte der Zeit bis zu diesem Zeitpunkt.
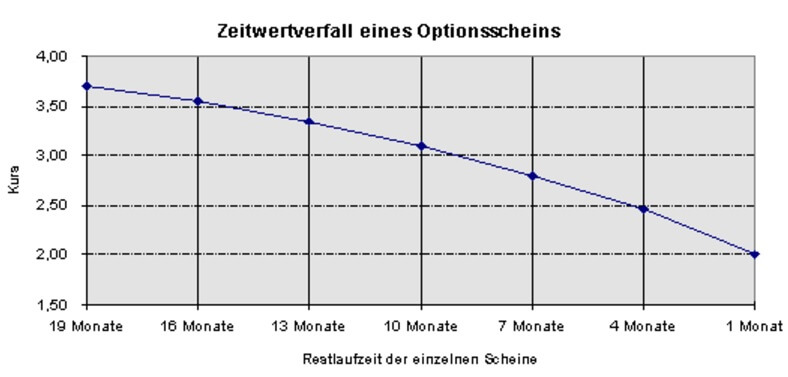
In der folgenden Grafik ist der Zeitwertverfall eines Optionsscheins dargestellt. Dazu wurden die Kurse mehrerer Optionsscheine mit gleichem Basiswert (US-Dollar) und gleichem Basispreis (1,70 DM), aber unterschiedlicher Restlaufzeit verglichen. Jeder Knotenpunkt stellt einen Optionsschein dar. Es ist deutlich zu sehen, dass der Zeitwertverfall gegen Ende der Laufzeit zunimmt. Der Dollarkurs lag etwa bei 1,70 DM, alle Optionsscheine waren also in etwa „at-the-money“.
Auswirkung des Zeitwertverfalls
Das Vega
Es ist an der Zeit, ein paar erste Worte über das Thema Volatilität zu verlieren. Die Volatilität ist ein Maß für die Schwankungsbreite eines Wertpapiers. Eine hohe Volatilität bedeutet, dass das Wertpapier in seinem Kurs sehr stark schwankt (z. B. junge High-Tech-Unternehmen), eine niedrige Volatilität bedeutet, dass der Kurs prozentual nur wenig schwankt (z. B. Indizes, Währungen). Die Volatilität hat einen immensen und oft unterschätzten Einfluss auf den Preis eines Optionsscheins! Eine steigende Volatilität verteuert Optionsscheine – und zwar Calls wie Puts gleichermaßen! – , weil die Chancen auf Gewinne oder mögliche Ausübung bei stark schwankenden Werten größer sind.
Das Vega gibt an, um wie viel sich der Wert eines Optionsscheins ändert, wenn die implizite Volatilität um eine Einheit steigt. Ein Vega von 0,27 bedeutet, dass der Optionsschein allein durch einen Anstieg bzw. Rückgang der Volatilität um einen Punkt um 0,27 Euro steigt bzw. fällt. Das Vega sollte bei der Auswahl eines Optionsscheins nicht außer acht gelassen werden. In Zeiten hoher Volatilitäten sollte man ein niedriges Vega wählen, weil dann die Gefahr eines Kursverlustes durch wieder sinkende Volatilität geringer ist. In Zeiten sehr niedriger Volatilitäten dagegen kann man ruhig Scheine mit einem hohen Vega kaufen, da eine mögliche steigende Volatilität zusätzliche Kursgewinne verspricht. Mathematisch ist Vega die erste Ableitung des Optionspreismodells nach der Volatilität. Ich werde im nächsten Teil auf den Unterschied und die Bedeutung von historischer und impliziter Volatilität eingehen, will nun aber noch die wichtigsten weiteren Kennzahlen kurz angeben.
Das Rho
Das Rho gibt an, wie stark sich der Kurs des Optionsschein ändert, wenn sich der risikolose Kapitalmarktzins um eine Einheit verändert. In den westlichen Industriestaaten gehen Zinsveränderungen jedoch in der Regel sehr langsam vonstatten, zudem ist der Einfluss der Zinsen im Optionspreismodell eher gering, so dass diese Kennzahl bei der Auswahl eines Optionsscheins kaum eine Rolle spielen sollte. Mathematisch ist Rho die erste Ableitung des Optionspreismodells nach dem Zinssatz.
Das Gamma
Das Gamma gibt an, wie stark sich das Delta verändert, wenn sich der Kurs des Basiswerts um eine Einheit erhöht. Nehmen wir an, ein Call-Optionsschein auf eine Aktie hat ein Delta von 0,38 (38 %) und ein Gamma von 0,04. Ein Anstieg der Aktie um 1,00 Euro hätte dann eine Veränderung des Delta um 0,04 auf 0,42 (42 %) zur Folge. Auch diese Kennzahl ist für den Anleger nicht zwingend erforderlich, sie ist vor allem – wie auch und vor allem das Delta – wichtig für den Emittenten zur Absicherung der verkauften Optionsscheinpositionen. Mathematisch ist Gamma die zweite Ableitung des Optionspreismodells nach dem Kurs des Basiswerts.
Damit will ich nun das umfangreiche Kapitel der Kennzahlen vorerst abschließen. Es gibt noch viele weitere Kennzahlen, die aber entweder wenig aussagekräftig (Theoretischer Wert), für den Privatanleger nicht notwendig sind oder lediglich triviale Dinge in Zahlen ausdrücken (Moneyness, Parität).


